编程不止是一份工作,还是一种乐趣!!!
线性代数中最基本的概念是向量(vector),可以把它看作某个多维空间中的一个数据点。
二维向量(two-dimensional vector)是平面上相对于原点的一个点。换言之,可以把一个向量想象成平面上的一个直线箭头,从原点指向一个具体的点。一般将二维坐标写成经坐标和y坐标的有序数对(或者叫元组),比如(6, 4)。
向量加法很简单:给定两个输入向量,将它们的x坐标相加,得到新的x坐标,然后将它们的y坐标相加,得到新的y坐标。举个例子,因为4 + (-1) = 3以及3 + 1 = 4,所以(4, 3) + (-1, 1) = (3, 4)。
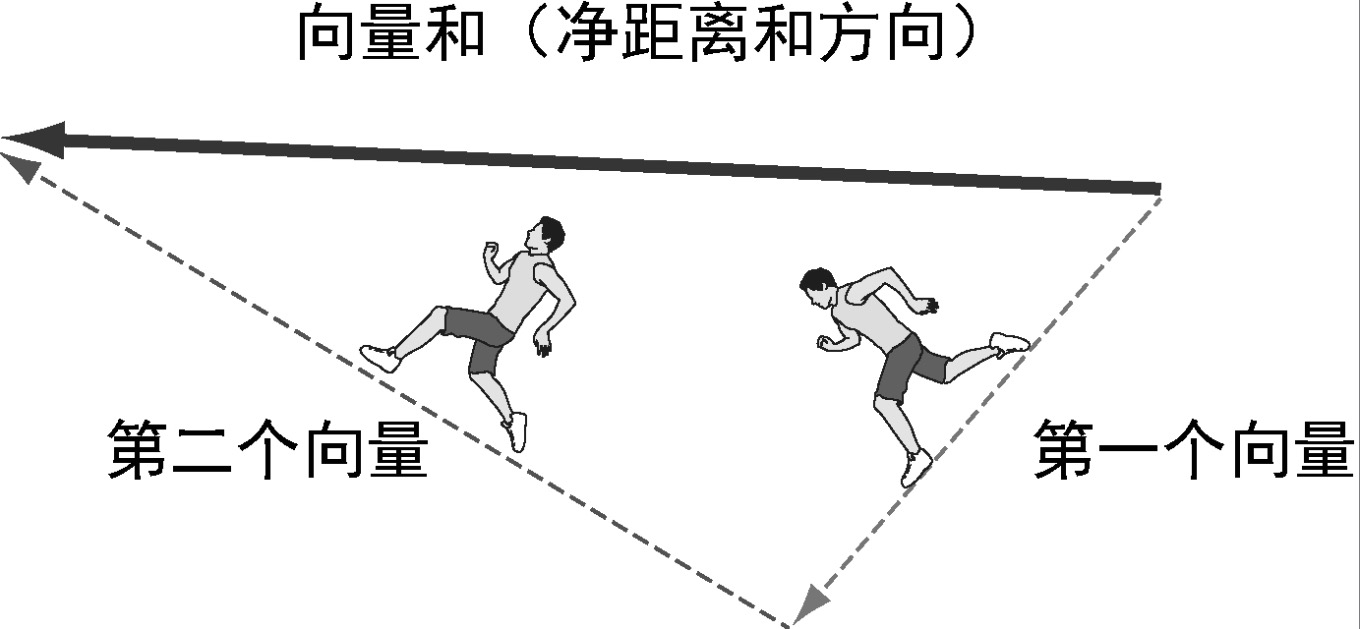
箭头形式的向量加法有时被称为首尾加法。这是因为如果把第二个箭头的尾部移到第一个箭头的头部(不改变其长度或方向),最终的向量和就是一个从第一个箭头起点到第二个箭头终点的箭头。

如果你在一个方向上移动一段距离,在另一个方向上又移动了一段距离,那么向量和可以表示移动的整体距离和方向。
(4, 0)和(0, 3)这两个向量分别称为(4, 3)的x分量和y分量。将一个向量分解成两个分量是很容易的,因为总能找到一个对应的直角三角形。如果知道各分量的长度,就可以计算出斜边的长度,也就是向量的长度。
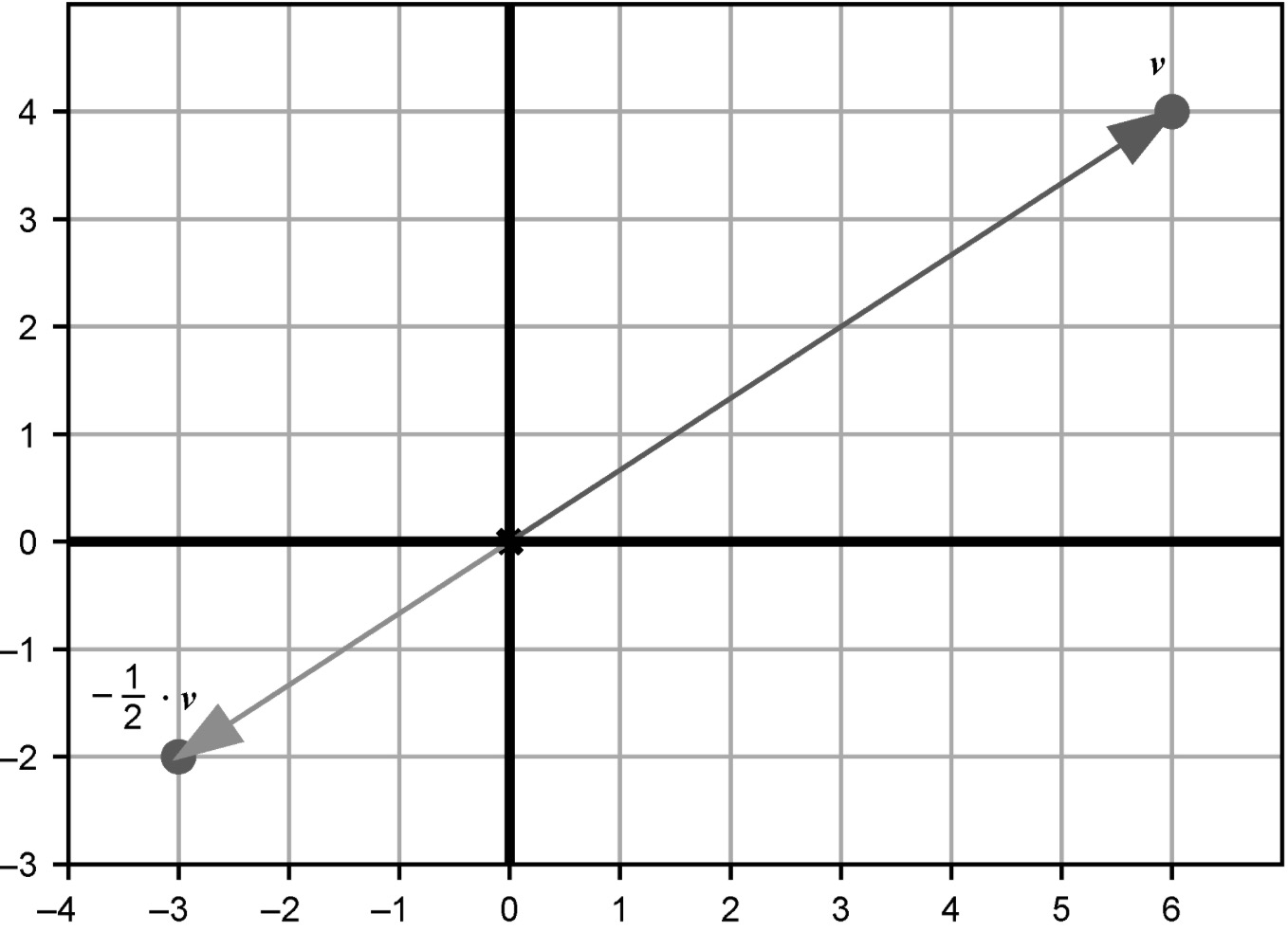
将向量乘以数的运算称为标量乘法。处理向量时,普通的数通常被称为标量(scalar)。scalar这个名字非常贴切,因为运算的效果是将目标向量按给定的系数进行缩放(scale)。对应到向量分量上,每个分量都按相同的系数进行缩放。可以把标量乘法想象成改变了一个由向量及其分量所定义的直角三角形的大小,但不影响其长宽比。
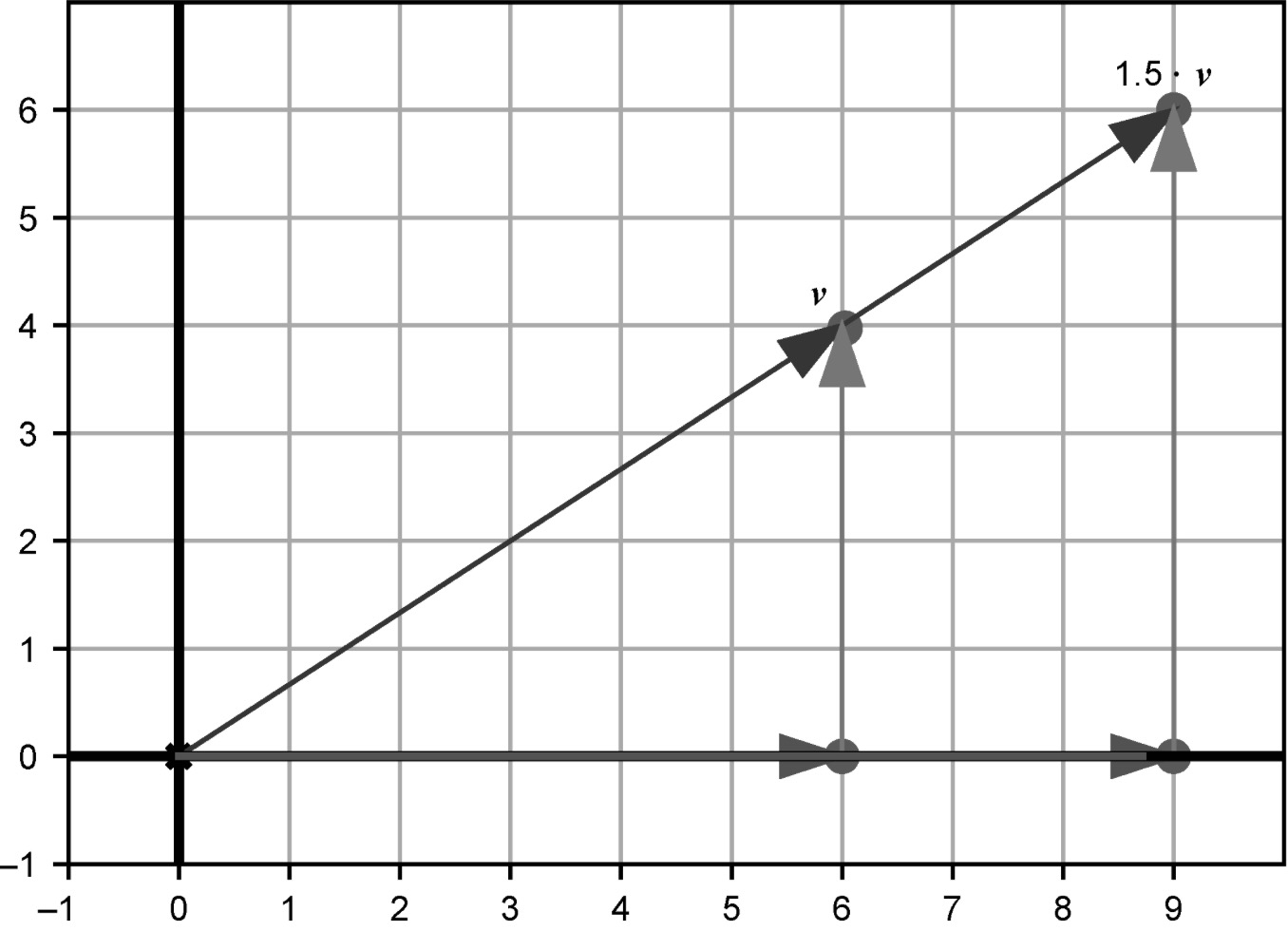
在坐标系中,用标量1.5和v = (6, 4)相乘,可以得到一个新的向量(9, 6),其中每个分量都是其原始值的1.5倍。这里测试了可以使用分数作为标量,还可以使用负数。如果原始向量是(6, 4),那么该向量的-1/2倍是多少?答案是(-3, -2)。这个向量的长度是原向量的一半,而且指向相反的方向。
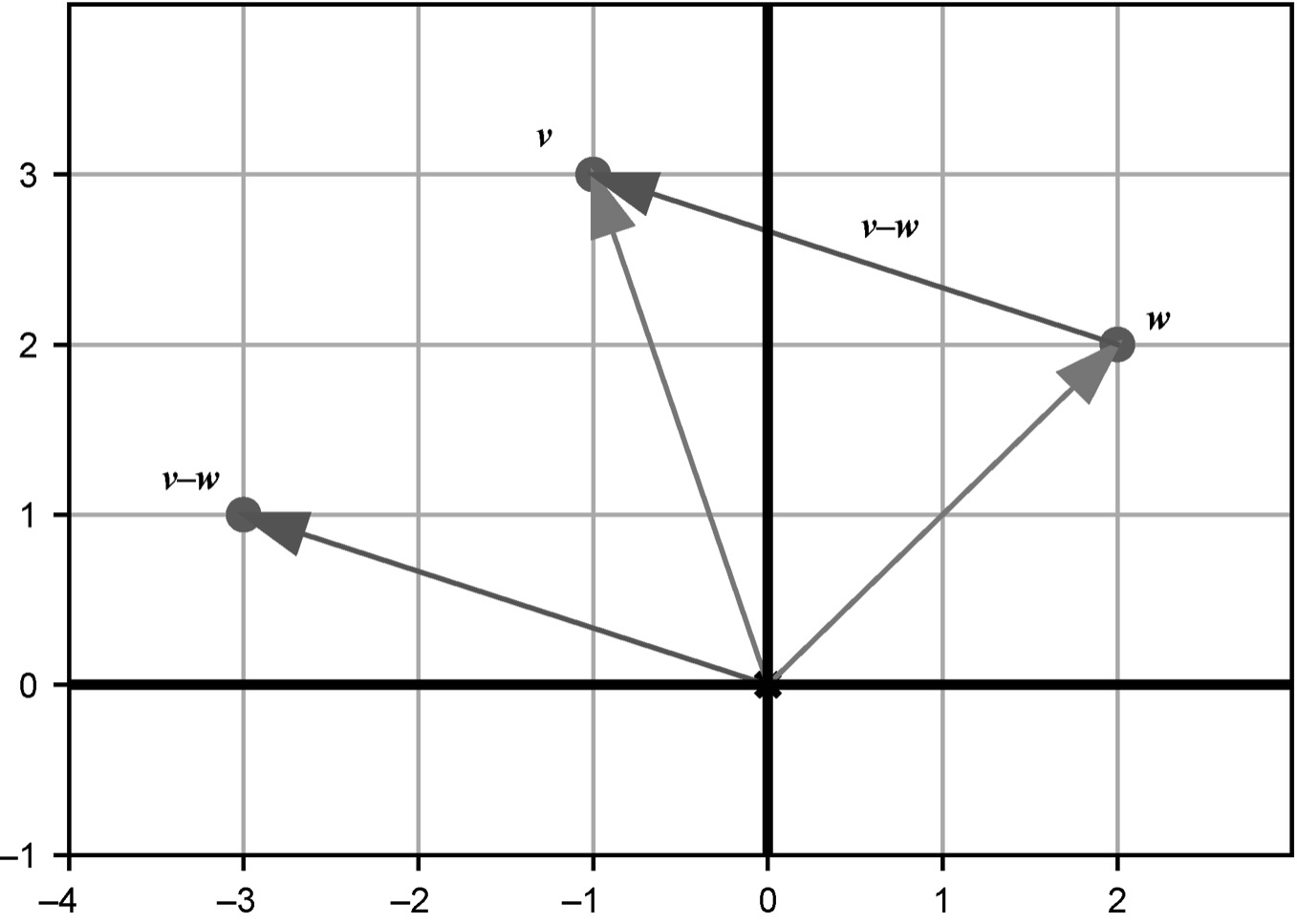
如果把v和w看作从原点开始的箭头,v - w是从w头部到v头部的箭头。v - w的坐标是v和w的坐标差。v = (-1, 3),w = (2, 2)。因此,v - w的坐标为(-1 - 2, 3 - 2) = (-3, 1)。v - w = (-3, 1)表示从w点开始,需要向左走3个单位、再向上走1个单位,才能到达v点。这个向量被称为从w到v的位移。位移是一个向量,而距离是一个标量。
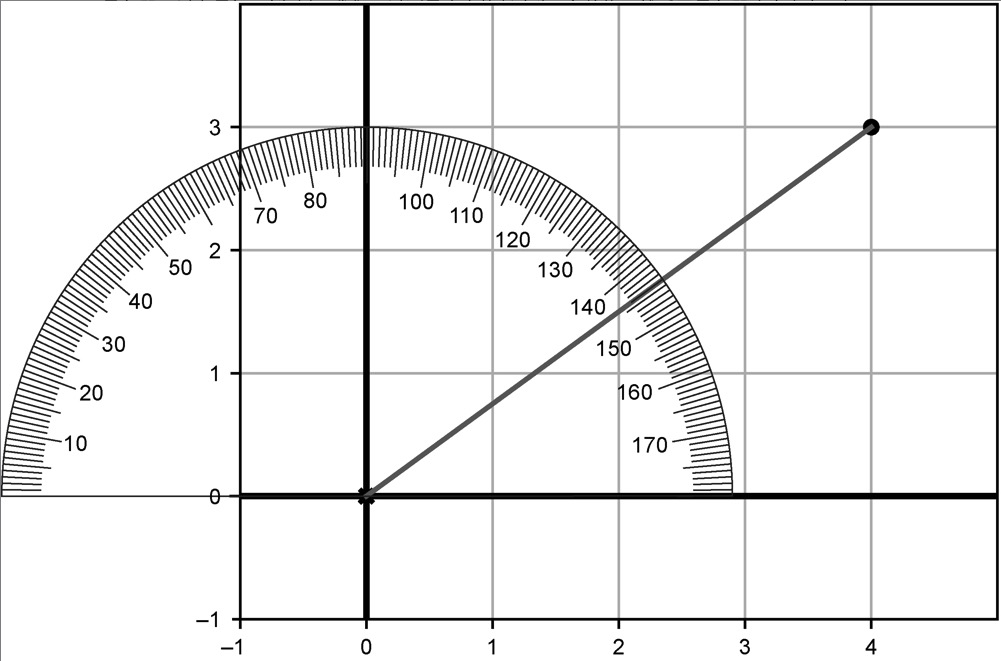
像原始坐标对一样,可以用一个新的数对(5, 37°)唯一地确定该向量。这种形式的坐标称为极坐标(polar coordinates),和我们到现在为止所使用的笛卡儿坐标(Cartesian coordinates)一样,能很好地描述平面上的点。有时候,比如做向量加法时,使用笛卡儿坐标更简单;而其他时候,极坐标更实用,特别是进行向量旋转时。
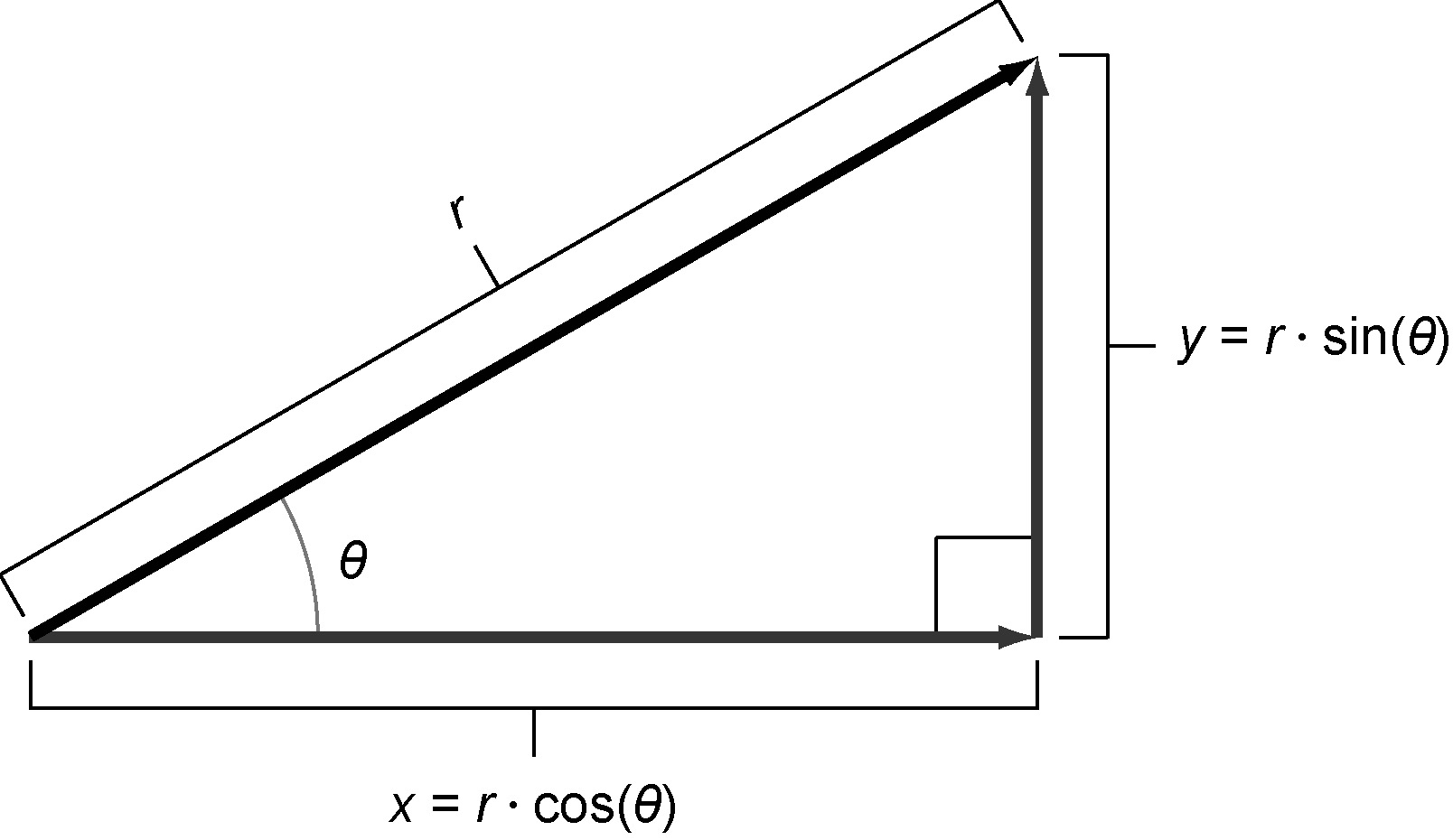
将极坐标转换为对应的笛卡儿坐标的一般方法。如果知道一个角 $\theta$的正弦和余弦,以及在该方向上的距离r,则笛卡儿坐标为$(r \cdot cos(\theta), r \cdot sin(\theta))$。
Python的math.atan2函数接收平面上一个点的笛卡儿坐标(按相反的顺序)作为参数,返回对应的弧度
def to_polar(vector):
x, y = vector[0], vector[1]
angle = atan2(y,x)
return (length(vector), angle)
Python不使用角度,事实上大多数数学家也不使用角度。他们使用弧度(radian)来替代角度,换算系数是:
之所以这样,是因为一个特殊的数π,它的值约为3.141 59。正是它搭建了角度和弧度之间的桥梁。
\[\pi = 180°\] \[2\pi = 360°\]用笛卡儿坐标移动(或平移)向量集合很容易,而在极坐标中就不那么自然了。不过,由于极坐标包含角度信息,会使得旋转向量更为方便。
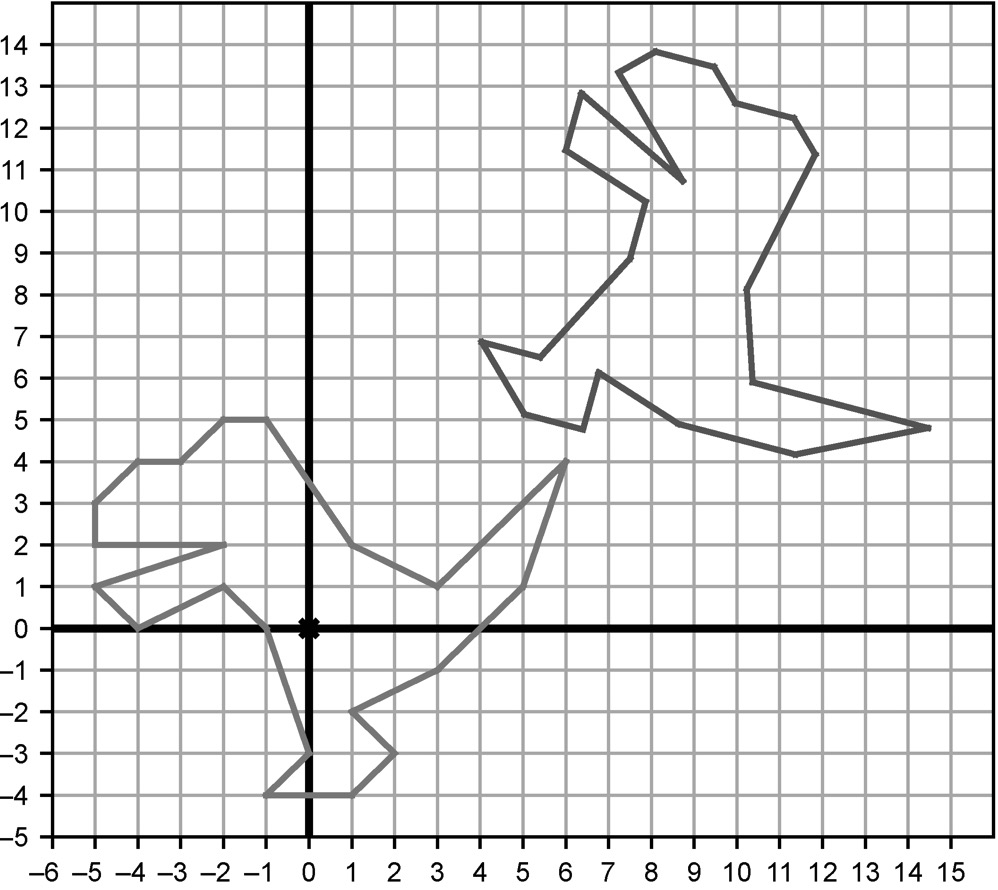
到目前为止,我们已经学习了如何平移、缩放和旋转向量。将这些变换应用于向量的集合,会对这些向量在平面上定义的形状产生同样的效果。当依次应用这些向量变换时,效果会非常惊人。例如,我们可以先旋转恐龙,然后平移。使用练习中的translate函数和rotate函数,可以很方便地实现平移和旋转的效果。
from math import sqrt, sin, cos, atan2
def add(v1,v2):
return (v1[0] + v2[0], v1[1] + v2[1])
def subtract(v1,v2):
return (v1[0] - v2[0], v1[1] - v2[1])
def add(*vectors):
return (sum([v[0] for v in vectors]), sum([v[1] for v in vectors]))
def length(v):
return sqrt(v[0]**2 + v[1]**2)
def distance(v1,v2):
return length(subtract(v1,v2))
def perimeter(vectors):
distances = [distance(vectors[i], vectors[(i+1)%len(vectors)])
for i in range(0,len(vectors))]
return sum(distances)
def to_cartesian(polar_vector):
length, angle = polar_vector[0], polar_vector[1]
return (length*cos(angle), length*sin(angle))
def to_polar(vector):
x, y = vector[0], vector[1]
angle = atan2(y,x)
return (length(vector), angle)
def rotate(angle, vectors):
polars = [to_polar(v) for v in vectors]
return [to_cartesian((l, a+angle)) for l,a in polars]
def translate(translation, vectors):
return [add(translation, v) for v in vectors]
def scale(scalar, vectors):
return [(scalar * v[0], scalar * v[1]) for v in vectors]