编程不止是一份工作,还是一种乐趣!!!
可以说,所有二维向量也都存在于三维空间中,它们的大小和方向不变,但被固定在一个高度z为零的平面上。下图显示了被嵌入三维空间的向量(4, 3)的二维图形,它的特征与之前相同。右图对所有仍然保持不变的特征添加了注释。
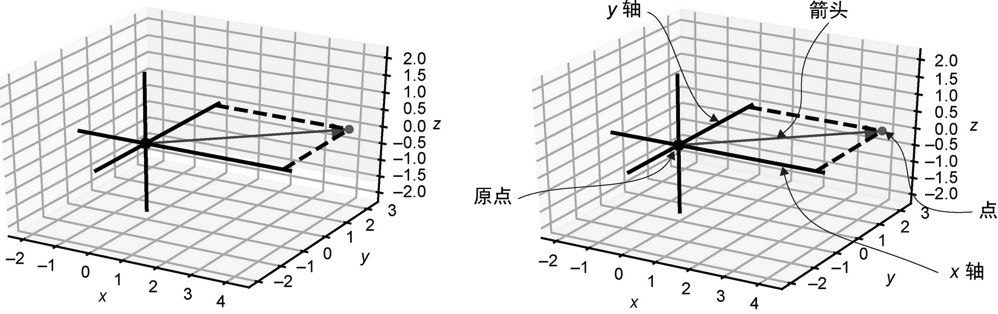
要在三维空间中指定唯一的点,总共需要三个数。像(4, 3, 5)这样的三元数对在三维空间中称为向量的x坐标、y坐标和z坐标。
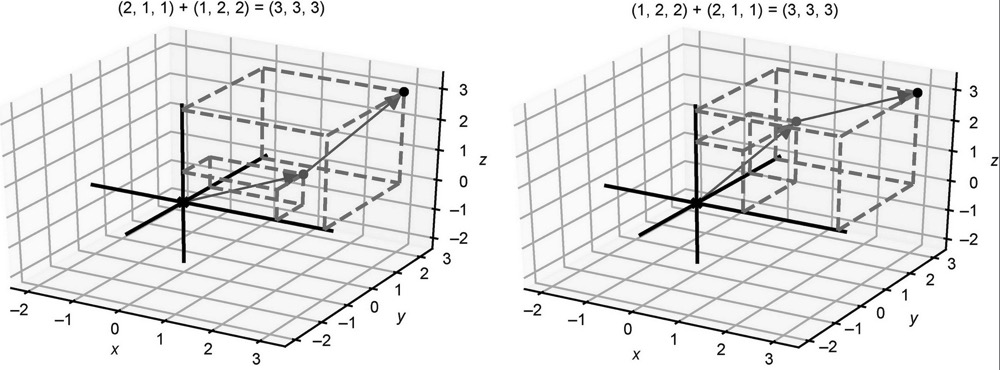
在三维空间中,向量加法仍可以通过将坐标相加来完成。向量(2, 1, 1)和(1, 2, 2)相加为(2+1, 1+2,1+2) = (3, 3, 3)。从原点开始,将两个输入向量首尾相接,就可以得到求和之后的点(3, 3, 3)。
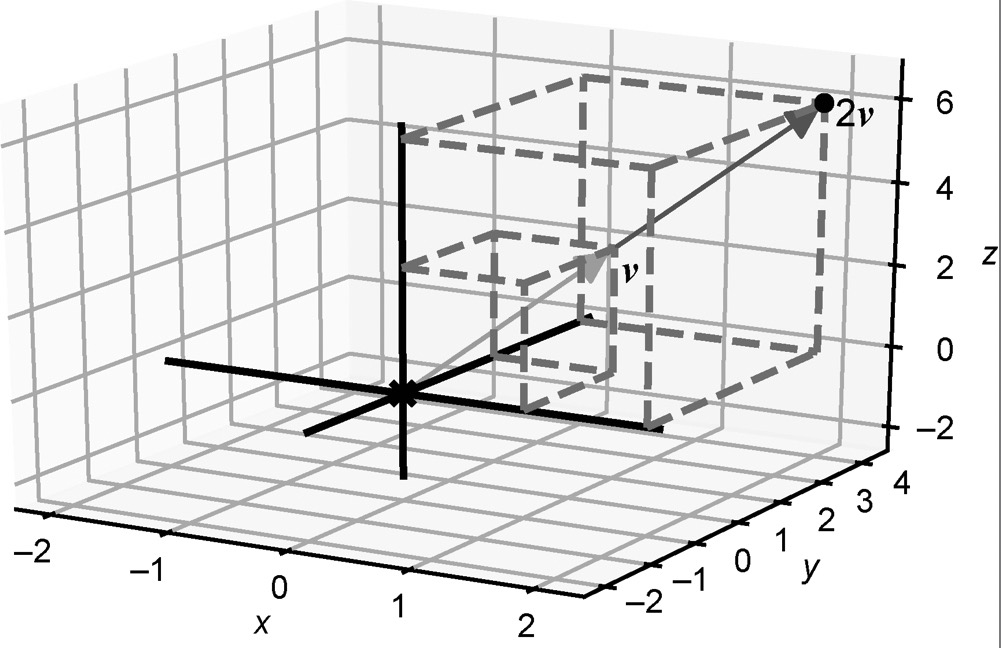
将三维向量乘以标量,就是把其所有分量乘以标量系数。例如,向量(1, 2, 3)乘以标量2,会得到(2, 4, 6)。由此产生的向量长度是原来的两倍,但两者指向相同的方向。图3-17显示了v = (1, 2, 3)和它的标量乘积$2 \cdot v = (2, 4, 6)$。
在二维平面上,两个向量v和w的差值就是“从w到v”的向量,称为位移。在三维空间中也是一样的,换句话说,v - w就是从w到v的位移,把这个向量与w相加即可得到v。将v和w看作从原点出发的箭头,那么v - w的差值也是一个箭头,它的头部位于v的头部,尾部位于w的头部。
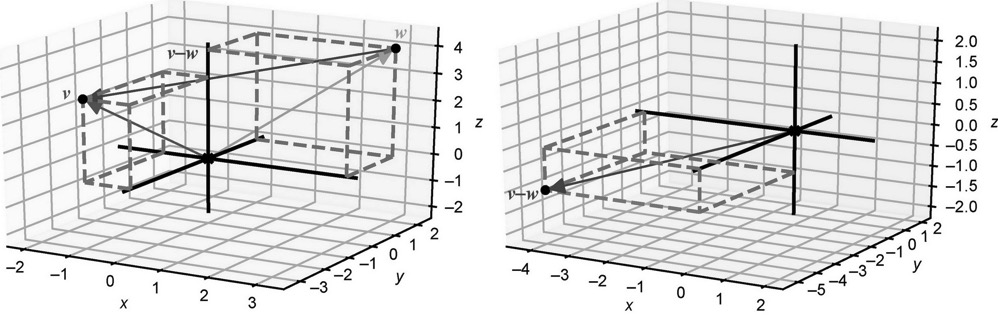
从向量v中减去向量w,在坐标上是通过取v和w的坐标之差来完成的。例如,v - w的结果是(-1 - 3, -3 - 2, 3 - 4) = (-4, -5, -1),这些坐标与上图中的v - w一致,表明它是一个指向负x、负y和负z方向的向量。
三维向量的长度公式:
\[长度 = \sqrt{x^2 + y^2 + z^2}\]它恰好和二维长度公式很相似。无论对于二维还是三维,向量的长度都是其分量平方和的平方根。
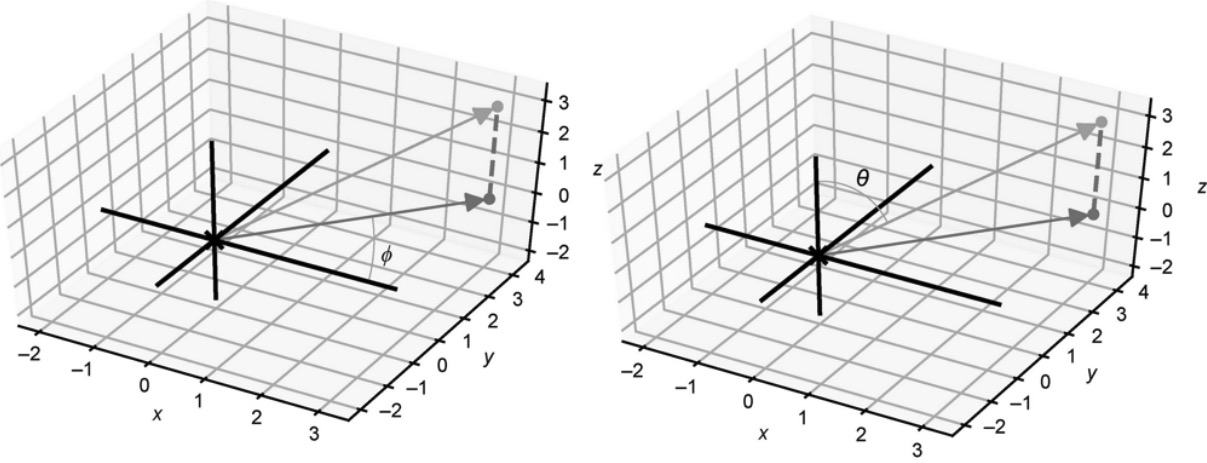
像二维向量一样,三维向量可以被看作箭头或者沿一定方向发生的一定长度的位移。在二维平面上,这意味着两个数(一个长度和一个角度,构成一对极坐标)足以指定任何二维向量。在三维空间中,一个角度不足以确定方向,但两个可以。
对于第一个角度,可以再次考虑没有z坐标的向量,就好像它仍然在xy平面上一样。另一种思考方式是,该角度是由来自非常高的z位置的光投射在向量上形成的阴影。这个阴影与x轴正方向形成一定的角度,类似于极坐标中的角度,并使用希腊字母$\phi$来表示。第二个角度是向量与z轴正方向的夹角,用希腊字母$\theta$用希腊字母来表示。
一种叫作点积,使用点运算符书写(例如,u $\cdot$ v);另一种叫作向量积(例如,u $\times$ v)。对于数来说,这些符号的意思是一样的,如3 $\cdot$ 4 = 3 $\times$ 4。对于两个向量来说,运算u $\cdot$ v和u $\times$ v不仅仅有不同的符号,而且代表的意义完全不同。
点积(也叫内积)是对两个向量的运算,返回一个标量。换句话说,给定两个向量u和v,那么u $\cdot$ v的结果是实数。点积适用于二维、三维等任意维度的向量。它可以被看作测量输入向量对的对齐程度。
指向相似方向的两个向量的点积为正,并且向量越大,乘积就越大。相反,如果两个向量指向相反或大致相反的方向,则其点积为负。
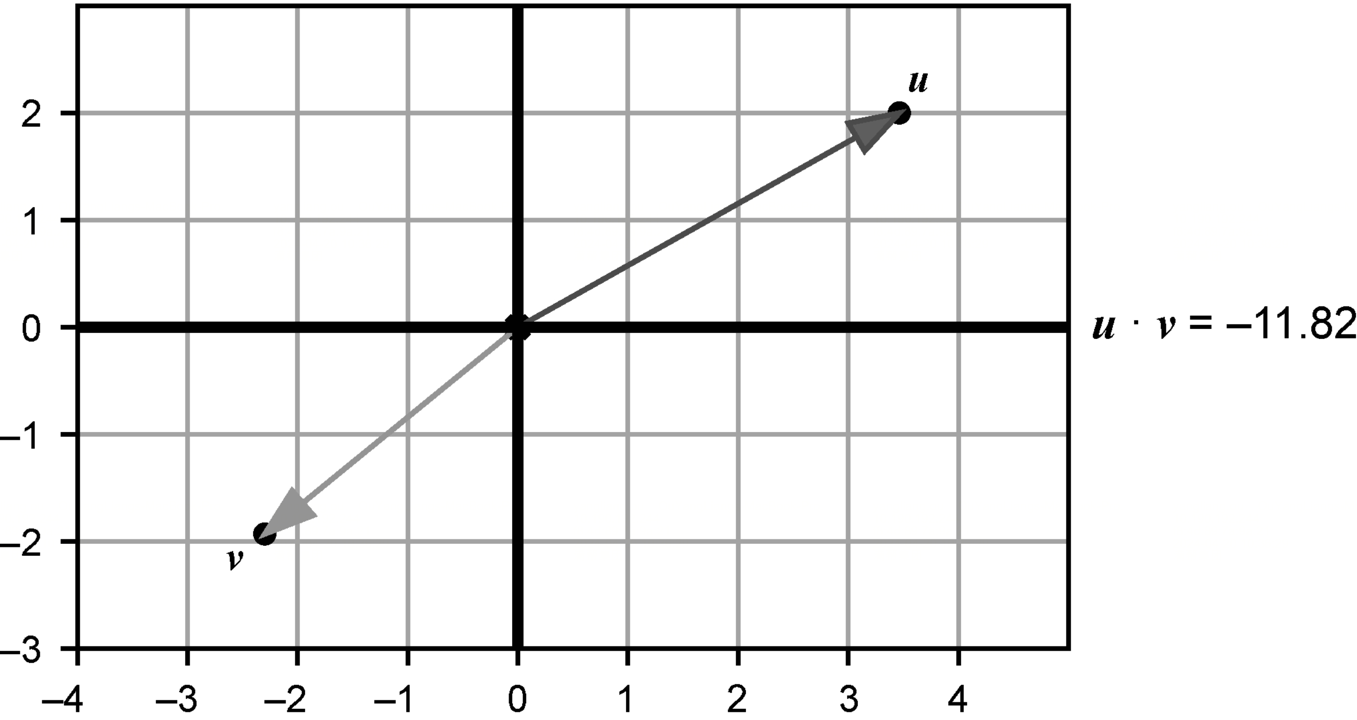
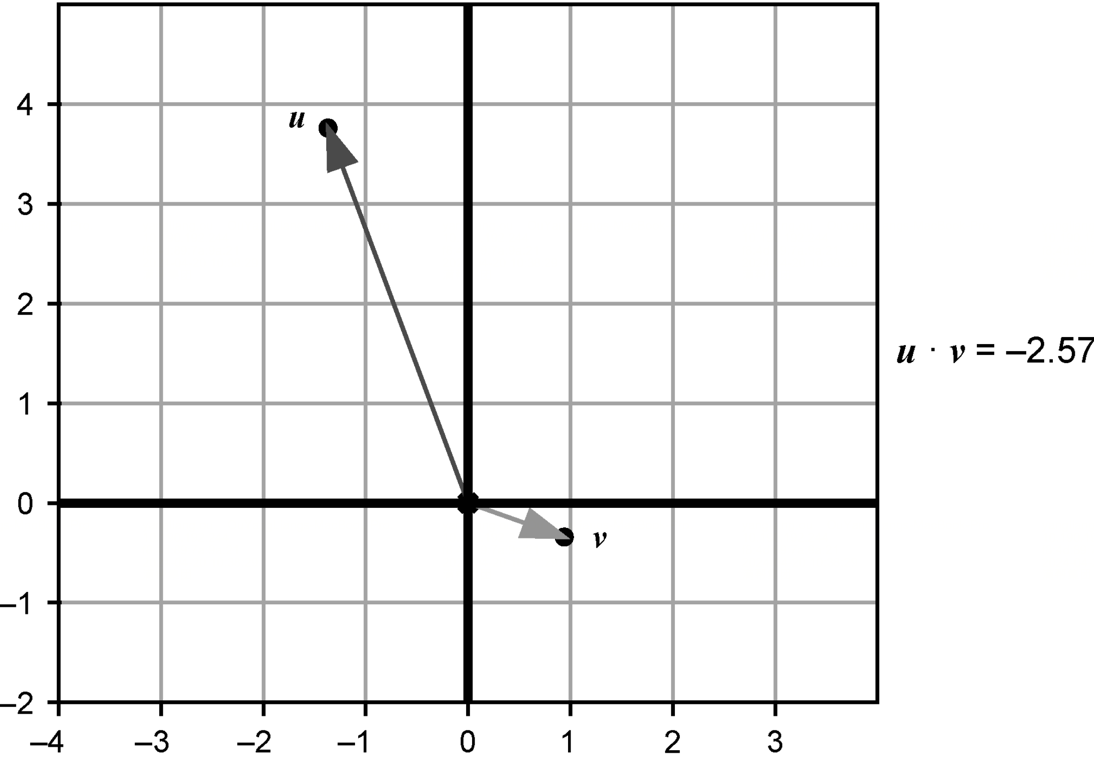
如果两个向量的方向完全垂直,那么无论它们的长度如何,点积都是零。这就是点积最重要的应用之一:在不做任何三角运算的情况下,计算两个向量是否垂直。如果两个向量的夹角小于90°,则向量的点积为正;如果夹角大于90°,则向量的点积为负。
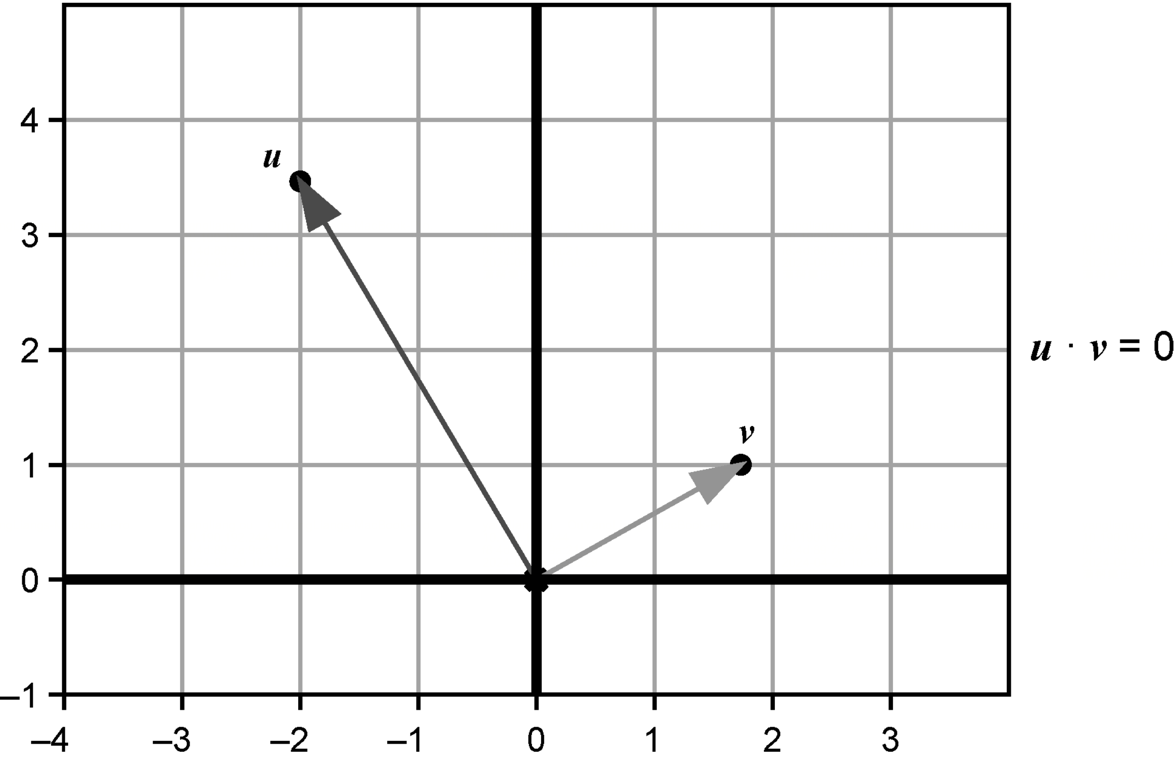
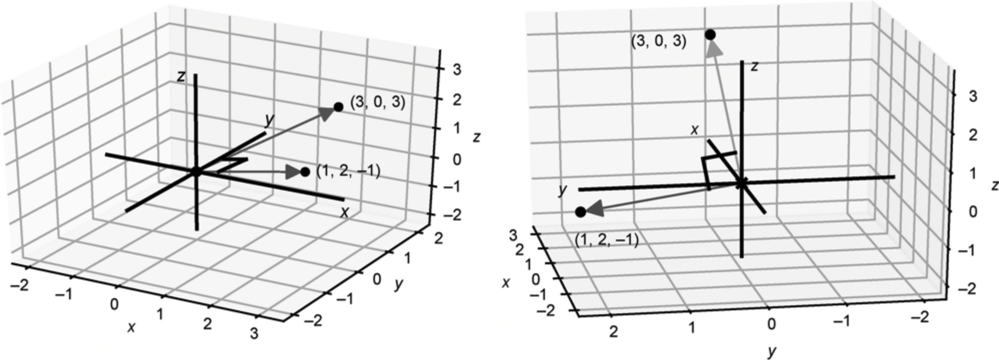
给定两个向量的坐标,有一个计算点积的简单公式:将相应的坐标相乘,然后将乘积相加。例如,在点积 (1, 2, -1) $\cdot$ (3, 0, 3) 中,x坐标的乘积为3,y坐标的乘积为0,z坐标的乘积为-3,因为相加为 3+ 0 + (-3) = 0,所以点积为零。这两个向量应该是垂直的。
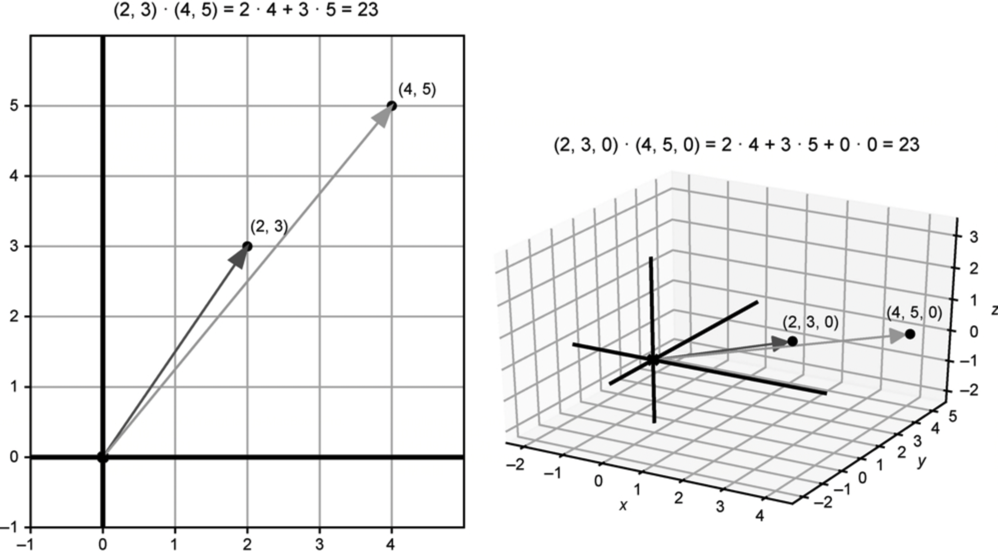
在三维空间中,我们的视角可能有误导性,这使得计算出向量的相对方向比目测更有价值。再看一个示例,下图显示了二维向量(2, 3)和(4, 5)在xy平面上具有相似的方向。x坐标的乘积是2·4 = 8,而y坐标的乘积是3·5 = 15。8 + 15 = 23就是点积的结果。这个结果是一个正数,证实了向量的夹角小于90°。它们在三维空间中可以表示为恰好位于z=0平面内的向量(2, 3, 0)和(4, 5, 0)。但是无论在二维平面还是三维空间中,它们的相对几何性质是不变的。
如果取同方向两个向量的点积,那么点积就等于两个向量长度的乘积。两个长度为5的向量的点积范围是-25~25:当它们指向相反方向时,点积为-25;当它们对齐时,点积为5·5 = 25。在3.3.5节的练习中你会发现,两个向量的点积范围是长度乘积到长度乘积的负值。
点积是根据两个向量的夹角而变化的。具体来说,当夹角角度为0到180°时,点积u $\cdot$ v的取值范围是u和v长度乘积的1到-1倍。我们已经见过具有这样特征的函数,即余弦函数。其实点积还有另一个公式。如果$\mid u \mid$和$\mid v \mid$分别表示向量u和v的长度,那么点积的计算公式为:$u \cdot v = \mid u \mid \cdot \mid v \mid \cdot \cos(\theta)$,$\theta$是向量u和v之间的角度。
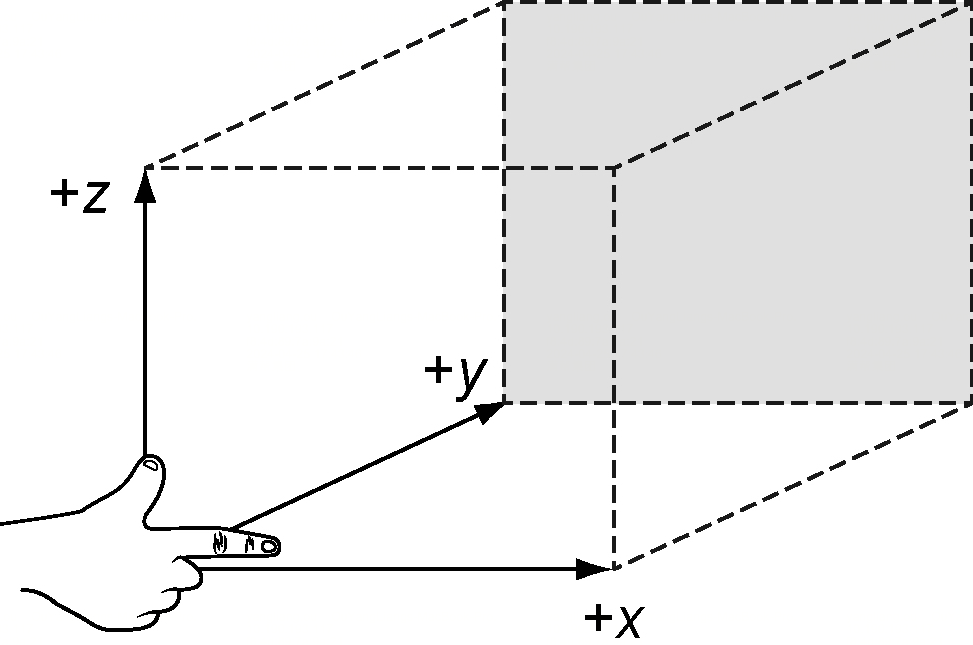
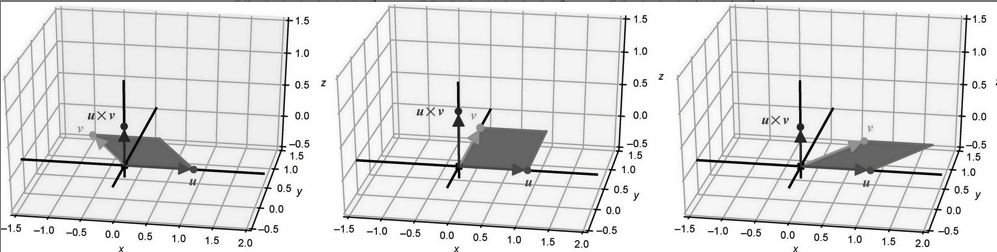
大多数数学家用手作为检测方向的现成工具。右手方向的规则如图所示:如果右手食指指向x轴正方向,中指、无名指和小指向y轴正方向弯曲,那么你的拇指就会指明z轴的正方向。
这就是右手规则,如果它与你的坐标轴一致,那么你就(正确地)使用了右手方向。已知两个输入向量,向量积的结果垂直于这两个向量。例如,如果u = (1, 0, 0),v = (0, 1, 0),那么向量积u $\times$ v恰好是(0, 0, 1),如图所示。
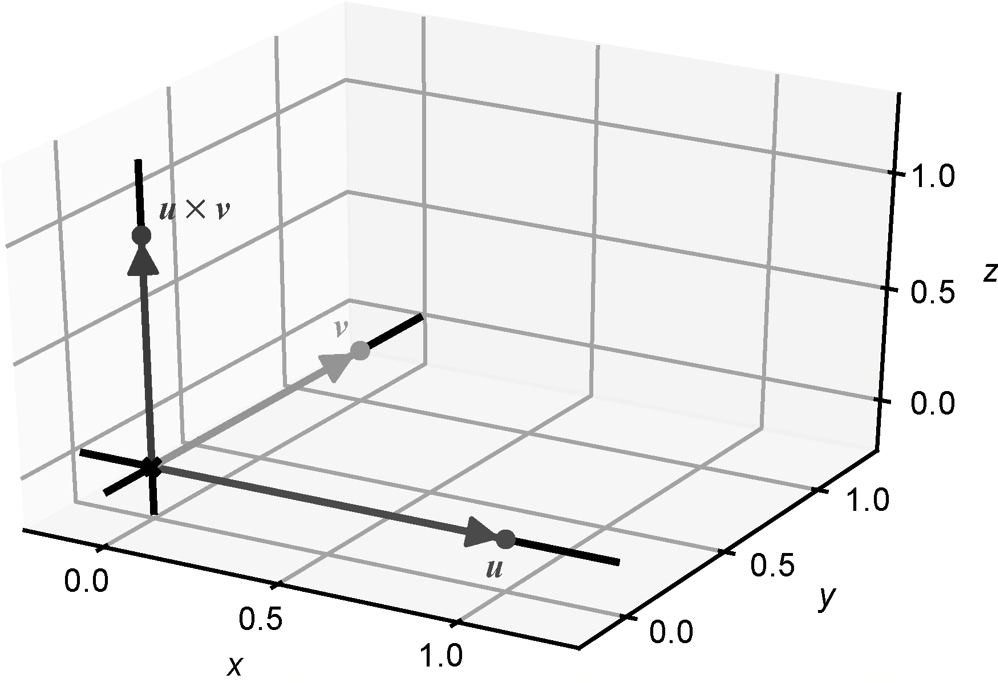
事实上,xy平面内任意两个向量的向量积都位于z轴上。这清楚地说明了为什么向量积在二维中不起作用:它返回的向量位于包含两个输入向量的平面之外。向量积的输出总是垂直于两个输入,即使输入并不在xy平面内也是一样。
但是有两个可能的垂直方向,向量积只能在其中之一上。例如,(1, 0, 0) $\times$ (0, 1, 0)的结果正好是(0,0, 1),指向z轴正方向。z轴上的任何向量,不管是正还是负,都垂直于这两个输入。为什么结果会指向正方向?这就是方向的作用:向量积也遵循右手规则。一旦你找到了垂直于两个输入向量u和v的方向,向量积u $\times$ v的方向就将三个向量u、v和u $\times$ v置于了右手系中。也就是说,我们可以将右手食指指向u的方向,将三指弯向v,拇指指向的就是u $\times$ v的方向。
和点积一样,向量积的长度也是一个数,它提供了关于输入向量的相对位置的信息。它测量的并不是两个向量的对齐程度,而更像是“它们的垂直程度”。更准确地说,它告诉我们两个输入之间的面积有多大。
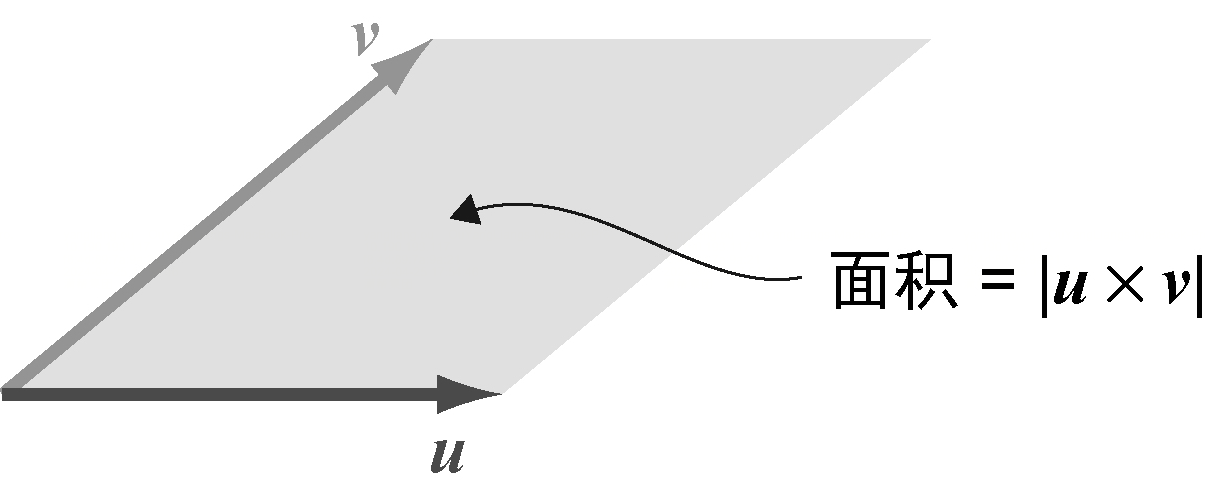
以u和v为边的平行四边形的面积等于向量积u $\times$ v的长度。对于给定长度的两个向量,在它们垂直时张成的面积最大。如果u和v在同一方向上,则张不成任何面积,向量积的长度为零。这是显而易见的:如果两个输入向量平行,则不存在唯一的垂直方向。
与结果的方向搭配,结果的长度能给我们一个精确的向量。平面上的两个向量保证有指向z轴正方向或负方向的向量积。可以看到,平面向量张成的平行四边形越大,向量积越长。
平行四边形的面积有一个三角公式:如果u和v的夹角为$\theta$,面积就是$\mid u \mid \cdot \mid v \mid \cdot sin(\theta)$。通过几何方法计算向量积是一种有良好定义的运算,但是这并不实用。一般来说,当向量并不总在坐标轴上时,要找到垂直结果所需的坐标并不容易。幸运的是,有一个明确的公式可以用输入坐标来计算向量积的坐标。
向量积的公式为:u $\times v = (u_yv_z - u_zv_y,\;u_zv_x - u_xv_z,\;u_xv_y - u_yv_x)$
如果用Python实现:
def cross(u, v):
ux,uy,uz = u
vx,vy,vz = v
return (uy*vz - uz*vy, uz*vx - ux*vz, ux*vy - uy*vx)