编程不止是一份工作,还是一种乐趣!!!
决策树
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题。
适用数据类型:数值型和标称型。
k-近邻算法可以很好地完成分类任务,但是它最大的缺点就是无法给出数据的内在含义,决策树的主要优势就在于数据形式非常容易理解。决策树的一个重要任务是为了数据中所蕴含的知识信息,因此决策树可以使用不熟悉的数据集合,并从中提取出一系列规则,在这些机器根据数据创建规则时,就是机器学习的过程。专家系统中经常使用决策树,而且决策树给出结果往往可以匹敌在当前领域具有几十年工作经验的人类专家。
在构造决策树时,我们需要解决的第一个问题就是,当前数据集上哪个特征在划分数据分类时起决定性作用。下表数据包含14个样本,特征包括:年龄(age)、收入(incoming)、是否是学习(student)、信用等级(credit_rating)。我们可以将这些样本分成两类:买电脑和不会买电脑。
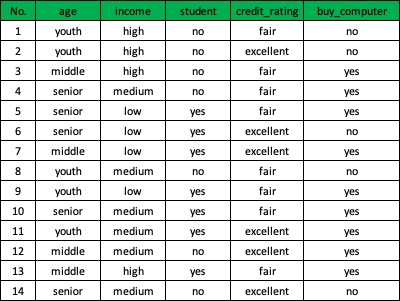
现在我们要决定依据哪一个特征来划分数据。在回答这个问题之前,我们必须采用量化的方法判断如何划分数据。在划分数据集之前之后信息发生的变化称为信息增益,知道如何计算信息增益,我们就可以计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。在可以评测哪种数据划分方式是最好的数据划分之前,我们必须学习如何计算信息增益。集合信息的度量方式称为香农熵或者简称为熵,这个名字来源于信息论之父克劳德·香农。为了计算熵,我们需要计算所有类别所有可能值包含的信息期望值,通过下面的公式得到:
\[H(x) = -\sum_{i=1}^n p(x_{i}) log_{2}p(x_{i})\]其中$p(x_{i})$是选择该分类的概率,n是分类的数目。对于上表中数据集D,有 9 个yes,5 个no,因此它的熵是:
\[H(D) = -\frac{5}{14}log_{2}\frac{5}{14}-\frac{9}{14}log_{2}\frac{9}{14} = 0.94\]熵越高,则混合的数据也越多。现在我们了解了如何度量数据集的无序程度,还需要划分数据集,度量划分数据集的熵,以便判断当前是否正确地划分了数据集。我们将对每个特征划分数据集的结果计算一次信息熵,然后判断按照哪个特征划分数据集是最好的划分方式,以age为例:
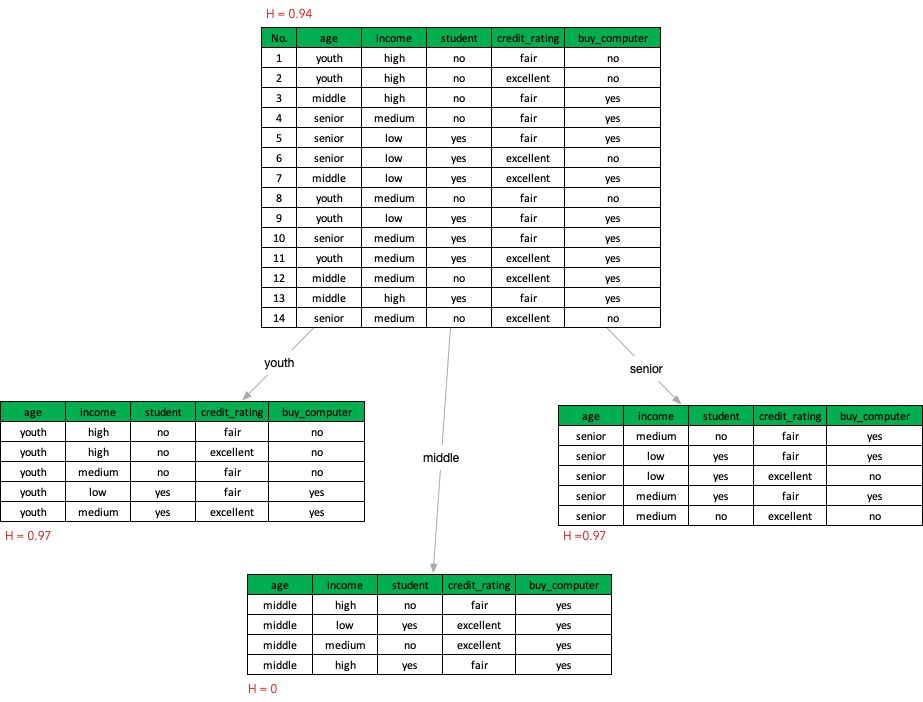
以age来划分数据集D后的条件熵为:
\[\begin{align*} H(D|age) &= \frac5{14}\times (-\frac25\log_2\frac25 - \frac35\log_2\frac35) \\ &+\frac4{14}\times (-\frac44\log_2\frac44 - \frac04\log_2\frac04) \\ &+\frac5{14}\times (-\frac35\log_2\frac35 - \frac25\log_2\frac25) \\ &=0.694 bits \end{align*}\]因此,根据age划分的信息增益就是:
\[gain(age) = H(D) - H(D|age) = 0.94 - 0.694 = 0.246\]如果以student来划分:
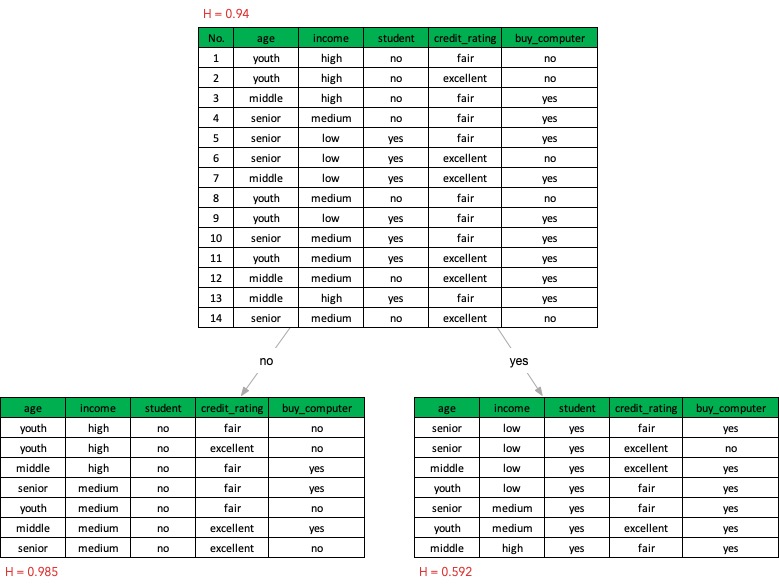
因为gain(age)大于gain(student),所以根据age特征来划分数据集D会比student要好。使用同样的方法对比所有的特征,就可以得出增益最大的特征,根据增益最大的特征来划分数据集;对于划分后的子数据集,再递归使用同样的算法,直到所有的特征都用完,或者对应的类别只有一种,就可以完成决策树的构造了。
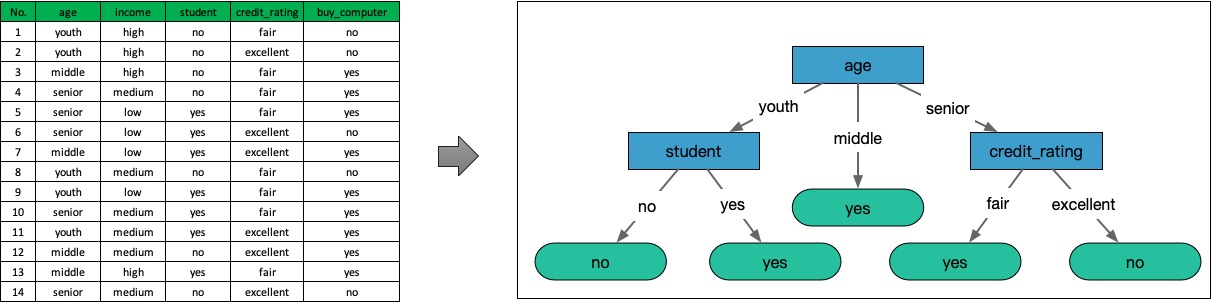
示例代码:点击这里